1.梯度定义

　　　　在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。比如函数f(x,y), 分别对x,y求偏导数，求得的梯度向量就是(∂f/∂x, ∂f/∂y)^T,简称grad f(x,y)或者▽f(x,y)。对于在点(x₀,y₀)的具体梯度向量就是(∂f/∂x₀, ∂f/∂y₀)^T.或者▽f(x₀,y₀)，如果是3个参数的向量梯度，就是(∂f/∂x, ∂f/∂y，∂f/∂z)^T,以此类推。

　　　　那么这个梯度向量求出来有什么意义呢？他的意义从几何意义上讲，就是函数变化增加最快的地方。具体来说，对于函数f(x,y),在点(x₀,y₀)，沿着梯度向量的方向就是(∂f/∂x₀, ∂f/∂y₀)^T的方向是f(x,y)增加最快的地方。或者说，沿着梯度向量的方向，更加容易找到函数的最大值。反过来说，沿着梯度向量相反的方向，也就是 -(∂f/∂x₀, ∂f/∂y₀)^T的方向，梯度减少最快，也就是更加容易找到函数的最小值

2.梯度下降的直观解释

　　　　首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。

　　　　从上面的解释可以看出，梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

3.梯度下降算法的推导

　　1.目标(损失，残差函数）：

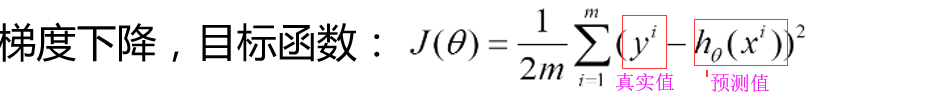
　注：为什么要除以m是因为求均值避免样本的个数对结果造成影响，除以2其实为了后面的求导做了方便(相当于优化）

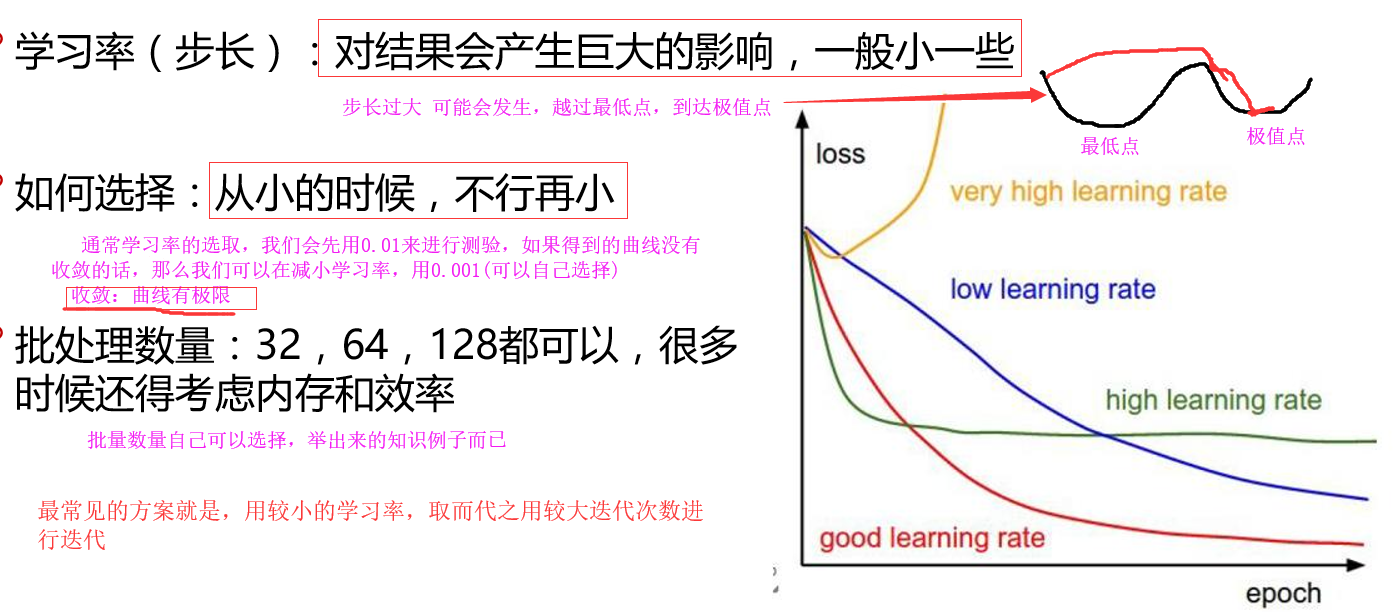
　　2.梯度下降的算法大家族

　　3.步长和批量的数量的选区

转载于:https://www.cnblogs.com/hum0ro/p/9650829.html

你可能感兴趣的文章